There is an english version available. There is also a translation to Thai.
En este artículo se presentan cuatro principios o leyes fundamentales: la relatividad, la incertidumbre, la incompletitud y la indecibilidad. Ellos fueron estudiados respectiamente por Albert Einstein, Werner Heisenberg, Kurt Gödel y Alan Turing. Esta es una explicación muy simple, sin detalles técnicos, pero que intenta reflejar la esencia de cada principio.
Relatividad

Esta sección ilustra el principio de la relatividad, que es más antiguo que la teoría de la relatividad de Einstein, y al final menciona una de las contribuciones de Einstein. La relatividad dice que no existe un punto de vista privilegiado, "objetivo", para hacer ciertas observaciones. Imaginemos que dos barcos se encuentran en altamar en una noche muy oscura, y sólo llevan una luz de posición en la punta del mástil. La noche está tan oscura que no es posible ver ni puntos en el horizonte ni ondas en el agua para saber hacia donde se mueve cada barco. En estas condiciones, cualquiera de los dos capitanes podría decir perfectamente que su barco es el que está "quieto", mientras el otro barco se está moviendo, o viceversa.
De la misma manera, desde hace cientos de años sabemos que la tierra no está "quieta" en el universo, sino que gira en torno al sol. Pero, ¿a qué velocidad se mueve el sol?. Necesitamos un marco de referencia para poder medir la velocidad. Podemos medir la velocidad del sol respecto a algún objeto distante, como otra estrella, el centro de la via láctea, el centro de nuestro grupo de galaxias, pero no existe algo que podamos llamar "la velocidad absoluta del sol". Claro, podríamos medir la velocidad del sol respecto al medio en que se desplaza, que no está exactamente vacío sino que tiene algunas particulas, pero esas partículas también se están moviendo. Queriendo determinar velocidades absolutas no llegamos a ninguna parte, siempre hay algún otro punto de vista que es igualmente válido y que entrega una velocidad totalmente distinta. La velocidad es relativa.
Ahora bien, si las cosas se mueven de forma relativa, entonces obviamente sus posiciones en cualquier momento también se miden relativas unas a otras. El universo, que sepamos, no tiene un "centro" que tenga características especiales, y si lo tuviera, claramente sería totalmente arbitrario decir que algo está "arriba", "abajo", "a la izquierda" o "a la derecha". En el espacio, estas cosas no tienen sentido. La posición y la dirección son también relativas.
Hasta aquí vamos bien, pero las cosas se complican un poco más. Pensemos un momento, ¿cómo medimos el tiempo?; lamentablemente, lo medimos con cambios de posición y de velocidad: el tiempo que tarda en caer una cierta cosa, el tiempo un rayo de luz en moverse entre dos puntos, etc. Una consecuencia directa de que posición y velocidad sean relativas, es que el tiempo también es relativo. No existe un "ahora" que sea simultáneo a todo el universo. No hay un gran reloj haciendo "tic-tac" para todos al mismo tiempo. El siguiente experimento se ha realizado en repetidas ocasiones: si ponemos dos relojes muy exactos a la hora, y luego los movemos entre sí, por ejemplo, con uno damos la vuelta al mundo en un avión mientras que el otro está "quieto", cuando los juntemos, para uno de los relojes habrá pasado más tiempo que para el otro. Si dejamos pasar más tiempo e incrementamos la velocidad, surge la típica imágen del astronauta que hace un viaje a las estrellas que para él dura pocos años, mientras que para los que se quedan en la tierra pueden pasar decenas o cientos de años. Mientras que la relatividad del movimiento en sí misma es un concepto bastante viejo, Einstein fue el primero en mostrar que incluso el tiempo no es absoluto, y que uno de las únicos invariantes que existen es la velocidad de la luz; dado que la velocidad de la luz es absoluta, el tiempo no lo es.
No confundir con subjetividad: en una película una vez escuché un diálogo así "para Einstein, todo era relativo, por ejemplo, media hora para tí con la persona amada o media hora esperando el metro no son lo mismo". Eso no es relatividad, eso se llama subjetividad y es otro cuento distinto. La relatividad dice que no existen puntos de vista privilegiados para observar la realidad, lo que puede interpretarse también como que la realidad es la suma de todos los puntos de vista posibles.
Incertidumbre

Si el Baseball se jugara con una pelota que fuera un poco más pequeña, del tamaño de una pelota de ping-pong, o una pelota que fuera un poco más grande, del tamaño de una pelota de volleyball, se vería raro pero se podría jugar perfectamente. Las reglas del juego a nuestra escala, son iguales para una pelota grande, mediana o pequeña. Incluso, podríamos arreglarnos para jugar un mini-baseball de mesa con diminutas pelotas de 1 milímetro de ancho. La dinámica del juego sería la misma siempre: la pelota se lanza, la pelota describe una curva, la pelota es golpeada.
Sin embargo, a la escala de lo muy pequeño, si continuamos y continuamos achicando la pelota hasta que sea del tamaño de un átomo o de un electrón, la situación cambia radicalmente. A escala atómica, ocurren todo tipo de cosas que nos parecerían muy raras. Un ejemplo de lo distintas que son las cosas cuando las vemos a escala atómica es el siguiente: si tenemos en nuestra casa una lámpara con un control para hacer la luz más brillante o más oscura, podemos controlar de forma muy fina cuánta luz hay en una habitación. Si la lámpara tiene una cierta luminosidad, nos da la impresión de que siempre podríamos bajarle un poco más la potencia sin llegar a apagarla completamente. Esto es solo una ilusión, porque si miramos con cuidado y tomamos una fuente de luz muy precisa, entonces veríamos que llega un punto en que si bajamos un poco más la luz, la apagamos, llega un momento en que no hay más puntos intermedios de luminosidad. La luz tiene una unidad mínima, indivisible, y toda forma de energía la tiene: se denomina un fotón. Todas las partículas subatómicas tienen una unidad mínima que se denomina "quantum", y un fotón es un quantum de luz. En atención a este fenómeno, la teoría que intenta explicar lo muy pequeño se denomina mecánica cuántica.
Volvamos al juego de baseball. Ahora ya no lanzamos una pelota de goma y cuero sino una partícula muy pequeña, digamos un electrón. Este electrón va camino a un diminuto bate de baseball con el que queremos golpearlo. Necesitamos saber donde viene el electrón, pero para verlo, necesitamos obviamente luz. El único problema es que la luz está hecha de fotones y el electrón es tan pequeño que los fotones lo desviarán. Apuntamos una diminuta linterna al electrón para verlo y recibimos los fotones de vuelta, pero para cuando recibimos los fotones ya hemos alterado la trayectoria del electrón. Podemos probar a usar un solo fotón pero eso es suficiente para desviar el electrón. Podemos probar a hacer que ese cuanto tenga menos capacidad de mover el electrón, es decir, menor momentum, pero el problema es que para ello la luz que produciríamos tendría ondas más largas y no nos permitiría ver bien donde está el electrón exactamente.
Heisenberg demostró que es posible construir un aparato que nos diga bastante bien donde está un electrón, pero que entonces no sabremos a qué velocidad se mueve. Si queremos medir su velocidad sin alterarla podemos usar una luz diferente pero entonces no veremos bien donde está. A escala atómica, ningún aparato puede decirnos al mismo tiempo exactamente dónde y exactamente a qué velocidad se está moviendo una partícula. Claro, podríamos intentar parar el electrón con una pared y así sabríamos donde está y sabríamos que está quieto respecto a la pared, pero eso no tiene ningún valor predictivo, y no sirve para nuestro juego de baseball. El punto es que al medir, introducimos una distorsión y que siempre tendremos que hacer ciertas concesiones en materia de qué tan preciso medimos estas cantidades. El principio de incertidumbre va más allá, y dice que en el fondo la posición del electrón está intrínsecamente indeterminada, y que su "posición" es solamente la probabilidad de obtener una cierta medición.
A veces se da otro ejemplo relacionado, pero que no alcanza a explicar la importancia de la incertidumbre: para medir la presión de los neumáticos de un automóvil, hay que dejar salir un poco de aire. Así que cuando el marcador dice 30,000 psi en realidad probablemente es más bien 29,999 psi o menos. Medir implica interactuar, e interactuar implica una cierta alteración. A nuestra escala esa alteración no importa, pero cuando vamos a lo muy pequeño, esa alteración es una parte muy importante de las reglas.
Notemos, de nuevo, que la incertidumbre no es solo algo relacionado con la medición, sino que intrínsecamente las partículas tienen cierto nivel de indeterminación. Incluso una medición "ideal" tendría indeterminación, porque la posición de la partícula es sólo la probabilidad de obtener una cierta medición, no una cantidad absoluta.
Incompletitud

En nuestra vida normal, hay muchas situaciones que tienen dos estados: si tengo que tomar un tren a las 8 de la mañana, hay dos posibilidades: o tomo el tren, o lo pierdo; si apreto el interruptor de la luz, la luz o se enciende, o se apaga; el acusado de un crimen es culpable o inocente, y así sucesivamente. Esta lógica de verdadero o falso es central en las matemáticas. ¿Uno más uno es igual a dos? Verdadero. ¿Dos más dos es igual a cinco? Falso. No hay medias tintas.
Hay muchos fenómenos naturales que tienen estados intermedios, pero la lógica booleana se ocupa de los fenómenos en que solamente hay dos posibilidades: verdadero o falso, blanco o negro, cero o uno, encendido o apagado, etc. Esto no es una debilidad de la lógica, sino más bien una definición de su quehacer, tal como, por ejemplo, la botánica se ocupa de las plantas o la geología de las rocas, la lógica booleana se ocupa de cualquier cosa que sea expresable y que tenga dos estados.
La lógica proposicional es una disciplina muy antigua cuya herramienta fundamental es la deducción o lógica deductiva. Sea A=María murió asesinada con un cuchillo. B=Juan estaba en la casa de María a las 23:00 de anoche. C=María murió a las 23:01. D=Juan conocía a María. E=Se encontró un mechón de cabello de Juan en manos de María. F=Se encontró un cuchillo con huellas de Juan y sangre de María. A y B y C y D y E y F implican: Juan es culpable. Si tomamos G=Juan es zurdo y las puñaladas son diestras, entonces A y B y C y D y E y F y G implican: Juan es inocente. Varias premisas se componen para llegar a una conclusión.
Esta lógica deductiva, tipo Sherlock Holmes, es la que entrega las reglas para componer ciertos hechos y obtener ciertas conclusiones. Por ejemplo: si para que una idea sea cierta, se necesario que otras dos cosas sean ciertas, y una de estas últimas resulta ser falsa, entonces la idea original no es cierta. Si para que haya nieve se necesita que llueva y haga frío, y no hace frío, entonces no habrá nieve. Lógico. Así como hay esta regla, existen muchas otras en la lógica proposicional que constituyen un sistema deductivo.
El sistema de lógica formal tradicional para trabajar sobre números naturales, está basado en la lógica proposicional más otras herramientas matemáticas. Si este sistema es completo, entonces cualquier cosa que sea verdadera es demostrable. Del mismo modo, cualquier falsedad es demostrablemente falsa. Gödel intuyó que este sistema no era completo, y se dedicó durante años al problema de encontrar una cosa, una sola cosa que estuviera dentro de los teoremas de los números naturales, pero fuera del alcance de las demostraciones en este sistema. Gödel buscó, dentro de la rígidez de las normas de la teoría de números en matemáticas, una expresión válida que no pudiera ser demostrablemente verdadera ni demostrablemente falsa.
Tomemos, por ejemplo, esta expresión, que no está bien definida pero es un buen ejemplo: "esta oración es falsa". Si "esta oración es falsa" es falsa, entonces, es doblemente falsa o sea verdadera ... y si "esta oración es falsa" es verdadera, entonces basta leerla para ver que es falsa. En teoría de números, Gödel encontró una forma de escribir (perdonen la sobresimplificación los matemáticos) una expresión p equivalente a "p no se puede demostrar". Esto es algo que es posible operar por medio de lógica deductiva, pero que en el fondo produce una cierta paradoja. Para hacerlo, tuvo que expresar muchas ideas en forma de números y desarrollar paso a paso una larga demostración, pero finalmente pudo demostrar que la teoría de números naturales era incompleta. Esto no está relacionado sólo con paradojas aparentes sino que va más allá: siempre existirán teoremas que jamás podremos demostrar que son ni verdaderos ni falsos.
La incompletitud de Gödel se puede entender como que cualquier sistema lógico deductivo consistente y suficientemente expresivo, no es completo, tiene "lagunas" llenas de expresiones que no se puede demostrar que sean ni verdaderas ni falsas.
Indecidibilidad

Alan Turing es considerado uno de los padres de la computación. A él se debe el modelo de cómo funciona un computador, que es fundamental para la ciencia de la computación. De acuerdo a este modelo, una sencilla calculadora de bolsillo o una sofisticada consola de videojuegos funcionan igual: leen unos pocos datos, revisan una tabla de reglas y una memoria y escriben unos datos de vuelta.
En una calculadora, lo que se lee es una tecla, la tabla de reglas son las operaciones matemáticas, la memoria es el resultado parcial y lo que se escribe de vuelta es el resultado final. En una consola de videojuegos lo que se lee es el estado del control o joystick, la tabla de reglas son los datos del juego, la memoria el estado del juego, y lo que se escribe son los dibujos en la pantalla. La memoria, por más grande que sea, nunca es infinita y el comportamiento de la máquina está totalmente determinado por las reglas que siempre debe obedecer de la misma manera, por lo que este modelo se conoce como "máquina de turing finita determinística".
Turing escribió muchos programas, incluso trabajó en descifrar códigos para los ejércitos aliados durante la segunda guerra mundial. Rápidamente se dió cuenta de que algunos programas se "colgaban" y se quedaban dando vueltas para siempre sin avanzar; esto sucedía a menudo cuando había alguna situación extraña en la entrada. Por ejemplo, es posible escribir un programa para descifrar códigos compuestos por números que representan las coordenadas donde se realizará un ataque, pero si a ese programa accidentalmente se le entregan letras en vez de números, entonces el programa falla, porque no está preparado para este tipo de entrada. Incluso resolviendo el problema trivial de aceptar solamente números, aparece un nuevo problema y es que las coordenadas pueden ser inconsistentes, por ejemplo, pueden representar un lugar más al norte que el polo norte, y así sucesivamente. Cada nuevo problema resuelto puede significar otros problemas en el programa.
Si queremos escribir un programa "perfecto", que nunca se cuelgue, entonces una forma de hacerlo es probarlo con todas las entradas posibles, pero esto muchas veces no es práctico porque hay demasiadas combinaciones; pero además de no ser práctico, tiene un problema más de fondo y es que aún cuando transcurra mucho tiempo nunca podemos saber si el programa está calculando todavía o si se ha quedado "colgado". Turing intuyó que este problema podía ser resuelto con ayuda de otros programas, y se dedicó a escribir un "superprograma" que fuera capaz de examinar otro programa y decir si estaba correcto, en el sentido de que terminaría alguna vez en lugar de quedarse colgado. Tras muchos intentos, comenzó a sospechar que tal vez no era posible escribir este superprograma, y finalmente pudo demostrar que en el caso general no es posible saber si un programa dado terminará o no en todos los casos. Para algunos programas se puede mostrar, por ejemplo, si escribimos un programa en particular que tenga una sola instrucción y que esta instrucción sea detenerse, ciertamente se podrá verificar, pero no es posible resolver el caso general.
El principio de indecidibilidad de Turing dice que no es posible escribir un programa que decida si otro programa cualquiera está correctamente escrito, en el sentido de nunca quedarse colgado. Esto plantea un límite a la verificación de los programas existentes hasta hoy, puesto que todos los intentos por construir computadores reales, usables en la práctica y que sean distintos a las máquinas de turing han resultado ser equivalentes en cuanto a su potencia pero también en cuanto a sus limitaciones. Es imposible construir una máquina que diga si un programa cualquiera se "colgará", lo que se intenta con las técnicas de programación modernas es conseguir que esto suceda con la menor frecuencia posible, como también que frente a un error la recuperación sea lo más rápida posible y sin ninguna pérdida de datos o funcionalidad y que el hecho de que un programa se cuelgue no implique que el computador entero deje de funcionar.
¿Un "punto ciego" ?
Estos principios fundamentales no deberían ser entendidos como limitaciones a la ciencia, ni tampoco como principios que excluyan la existencia de una realidad objetiva. Más bien son limitaciones a la lógica formal y a la forma en que hacemos observaciones, que tienen que ser tomadas en cuenta a la hora de entender los fenómenos naturales.
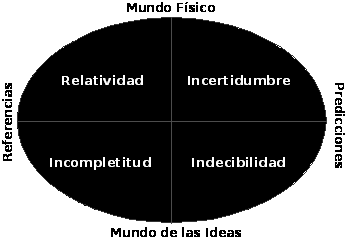
Estas cuatro leyes tienen cierta relación entre sí. Tanto la relatividad como la incertidumbre se originan en la física, mientras que la incompletitud y la indecidibilidad aparecen en la matemática. La incertidumbre y la indecidibilidad, a su vez, tienen que ver con la incapacidad de hacer predicciones, mientras que la relatividad y la incompletitud con el hecho de que las referencias son necesarias, pero impiden ciertas operaciones. No quisiera intentar llevar estas relaciones demasiado lejos: es probable que en el futuro descubramos nuevas limitaciones al quehacer científico, que completen esta imagen. Más bien, y para terminar, quisiera plantear otra analogía.
En el ojo de los mamíferos observamos una construcción bastante curiosa, y es que todos los nervios que van desde la superficie de la retina hasta el cerebro, al salir del ojo se encuentran en un solo punto. Este diseño tiene una desventaja y es que justamente el punto donde se encuentran los nervios no es sensible a la luz. Esto genera un "punto ciego", una zona del campo visual en la cual no vemos. Al mismo tiempo y curiosamente, no vemos que no vemos. Primero, el punto ciego es bastante pequeño; segundo, el cerebro compensa la imagen para que no veamos una pelota negra flotando en el aire, y tercero, tenemos dos ojos y sus puntos ciegos no coinciden. Podemos ocupar el hecho de que sabemos que hay un punto ciego en el diseño de algunos aparatos, por ejemplo, en el diseño del tablero de control de un avión, pero aparte de eso en la vida diaria y para el 99.9% de la población no tiene ninguna relevancia.
Sucede algo similar con las leyes que hemos discutido. Por una parte, restringen la mirada, pero podemos operar con ellas. Aún existiendo relatividad, si nos sorprenden a 120 kilómetros por hora en una zona de 100 km/hr tendremos una multa, sin importar que con relación a nosotros el automóvil estaba inmóvil, porque hemos fijado cierto marco de referencia. Aún existiendo incertidumbre es posible jugar al baseball porque la incertidumbre para un objeto del tamaño de una pelota es muchísimo menor que lo observable a simple vista. Aunque los sistemas deductivos son incompletos, la incompletitud le quita el sueño a muy pocos matemáticos, y cada año demostraciones increíblemente ingeniosas y difíciles son llevadas a cabo sin problemas. Aún existiendo indecibilidad, programas de primera calidad controlan sistemas de alta disponibilidad y la mayoría de los errores encontrados no provienen de oscuras condiciones de parada sino de meros descuidos a la hora de programar.
Las reglas del juego científico incluyen relatividad, incertidumbre, incompletitud e indecibilidad. Desde el punto de vista de la ciencia, el entender estas limitaciones nos puede llevar a nuevos descubrimientos acerca de cómo funciona el universo. Aún a través de este punto ciego, podemos ver.
Agradecimientos
Pepe Flores , ingeniero en computación y emprendedor, también mi profesor, mi jefe, mi socio y mi amigo, en ese orden cronológico, es de quien escuché primero la idea de que estas son las cuatro leyes más importantes que existen en la ciencia. Ingmar Weber y varios lectores de Kuro5hin también dieron aportes y comentarios muy interesantes.